オーダー記法とアルゴリズムの関係を解説！

いきなりですが、アルゴリズムはコンピュータの処理を短くするために使います。

同じ結果を得るのであれば、実行時間が短いアルゴリズムの方が優秀ですよね。

このアルゴリズムの優秀さを比較する方法として「オーダー記法」がありますので、今回はオーダー記法の考え方と使い方を解説します！

オーダーはコンピュータの計算量

オーダーは「アルゴリズムを完了するために必要な計算量」のことです。

例えば、あるデータ「1，3，5，６，7，９」の中に「７」があるかを探すアルゴリズムの時に、頭から一つずつ比較するアルゴリズムより、真ん中から比較するアルゴリズムの方が処理が短くなりますよね。

オーダーはこのアルゴリズムの計算量を表すために使い、このオーダーの記述方法を「オーダー記法」と呼びます。

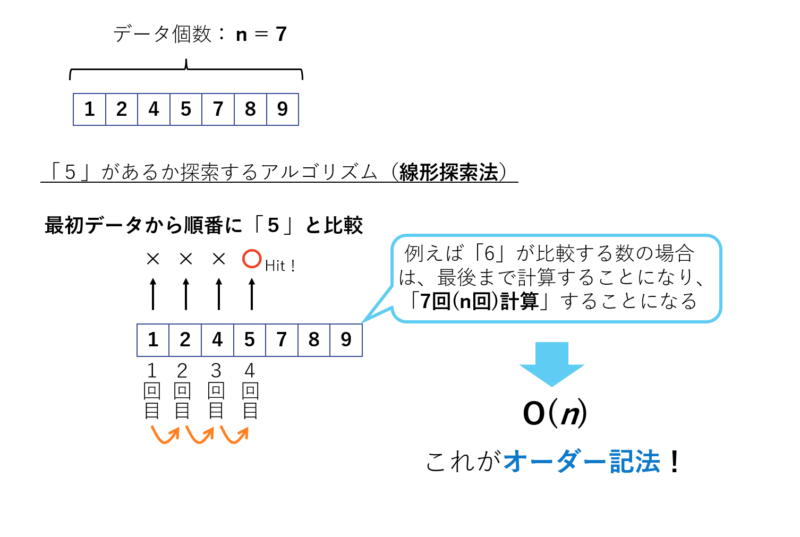
ちょっと分かり難いと思いますので、以下の図でも解説します。

では、このO(n)はどうゆう意味かというと、「データの個数nが2倍、3倍になると、アルゴリズムの計算量も2倍、3倍になる」ということです。

ということは、O(n²)の場合、「データの個数nが2倍、3倍になると、アルゴリズムの計算量は4倍、9倍になる」ということになりますね。

このことから、O(n²)はデータの個数が大きくなると指数関数的に計算量が増えてしまうので、O(n)に比べて実用的とは言えないアルゴリズムということになります。

またオーダーは「これ以上は大きくならない」という「最大の計算量」を表します。

例えばデータ個数nが「10」だとした場合、O(n)のアルゴリズムでデータを検索する際に計算量が必ず「10」になるわけではなく、3回目で目的のデータが検索で見つかったら、計算量「３」になる、ということを注意してください。

代表的なアルゴリズムのオーダー

では、いくつか代表的な探索アルゴリズムのオーダーがどうなるかを具体的に解説します。

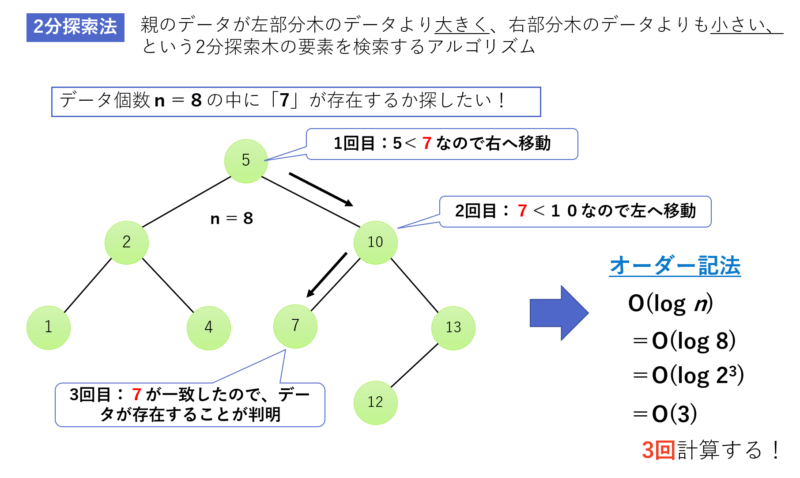
2分探索法

このアルゴリズムは、調べる範囲を半分に分割することで目的のデータを見つけることができます。

2分探索法には大きな前提があります。

下の図の例においてはデータ個数が「ｎ＝８」で、データが昇順で「1, 2, 4, 5, 7, 10, 12, 13」で整列されてます。

この状態を2分探索木なんて呼びますが、先ずデータの中央の「5」を検索したい数「7」と比較をします。その後、右部分木の親である「10」と比較し、左部分木の「7」が見つかり、データの中に検索した数字があったことが分かります。合計3回比較しましたね。

ここで2分探索法のオーダー記法は「O(log n)」となり、今回は「ｎ＝８」なので、上図の対数計算をした結果、オーダー（計算量）は「3回」となり、実際計算した回数を同じになります。

ハッシュ探索法

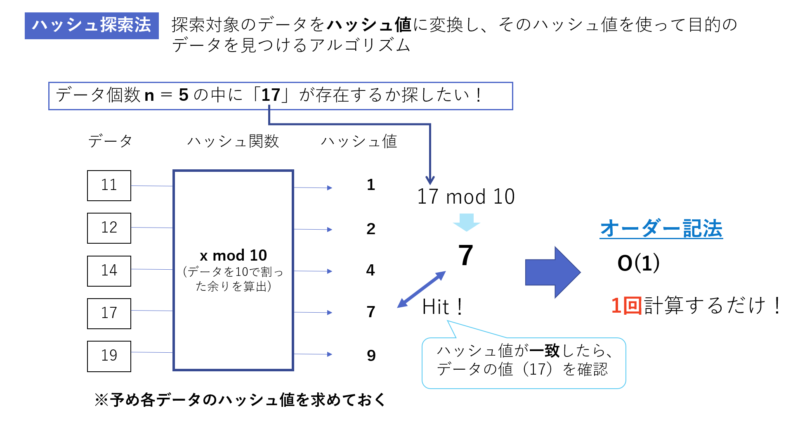
続いてハッシュ探索法ですが、このアルゴリズムは探索対象のデータをハッシュ値に変換し、ハッシュ値を使って目的のデータを見つけ出します。

ハッシュ探索法のイメージを下図に記載してます。

先ず、検索対象となるデータをハッシュ関数を使ってハッシュ値に変換します。上図の例だとハッシュ関数は「剰余」と呼ばれ、対象データを「10」で割って、その余りをハッシュ値と、そのハッシュ値を配列の添え字（インデックス）として、検索データを配列に格納します。

上図の例だと、[1]=11, [2]=12, [4]=14, [7]=17, [9]=19　となり、これを「ハッシュ表」と呼びます。

このハッシュ表を使うと、データの探索が非常に簡単になります。

例えばデータの中に「17」があるか調べるときに17を10で割った余りが「７」になるので、ハッシュ表の添え字が[7]の配列データを見てみます。そうすると「17」がヒットしますね。

ここでハッシュ探索法のオーダー記法は「O(１)」となり、探索における処理回数は「1回」ということになります。

これまでの例では検索対象のデータ個数が「ｎ＝5」ですが、これが「n＝100」だとしても探索の処理回数は「1回」ですので、データ個数に影響されないことがメリットですね。

これがハッシュ探索法におけるオーダー記法になります。

色々なアルゴリズムのオーダーの比較

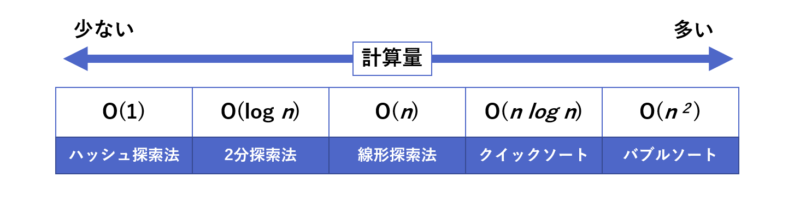
ここまで紹介した各アルゴリズムを計算量によって比較してみましょう。

以下に計算量の多さで並べてみました。

「クイックソート」や「バブルソート」は整列アルゴリズムと呼ばれる部類になります。

計算量が少ない方がもちろん良いですが、そのアルゴリズムでしかできないことも当然ありますので、あくまでも計算量の観点での比較なので、アルゴリズムそのものの優劣の比較では無い、ということは理解しておきましょう！

例えば、ハッシュ探索法はデータ個数がいくつでも、計算回数が「1回」なので、非常に優秀ですが、データの値が異なるのにハッシュ値が同じになってしまうケースが存在します。これを衝突と呼びます。

例えば上図の例だと、「17」も「27」も10で割ると余りが「7」なので、ハッシュ値が同じになっていまい、同じになってしまった場合に別の方法でこれを解決する必要が出てくるので、アルゴリズムの効率は落ちてしまいます。

まとめ

今回はオーダー記法に関して解説してきました。

オーダー記法はアルゴリズムの計算量を算出でき、データ個数に応じて、どのアルゴリズムを使うのが最適なのかを求めることができますね。

オーダー記法は慣れるまでちょっと時間が掛かりますが、アルゴリズムの仕組みと合わせて覚えると良いと思います。

以下記事で「そもそもアルゴリズムとは？」に関して解説していますので、併せて読んで頂ければと思います。

以上です！