いきなり「シフト演算とは!?」と言われても困るかと思いますが、今回はシフト演算を解説します。
「演算」という言葉があるので、計算するためのもの、というのは分かるかと思いますが、「シフト」という言葉が良く分からない...更には「論理シフト」と「算術シフト」なる言葉まで出てきます。
実はこのシフト演算はコンピュータの中で「掛け算や割り算」を行うために非常に重要になってくる演算方法なので、しっかり理解していきましょう!
シフト演算の役割とは?
コンピュータで「足し算」を行う時は2進数で表現した数字をANDやORの論理演算子を使って行います。「引き算」は引く数字をビット反転して2の補数にして、それを足すことで結果を得ることができます。
では「掛け算」はどうするのでしょうか?
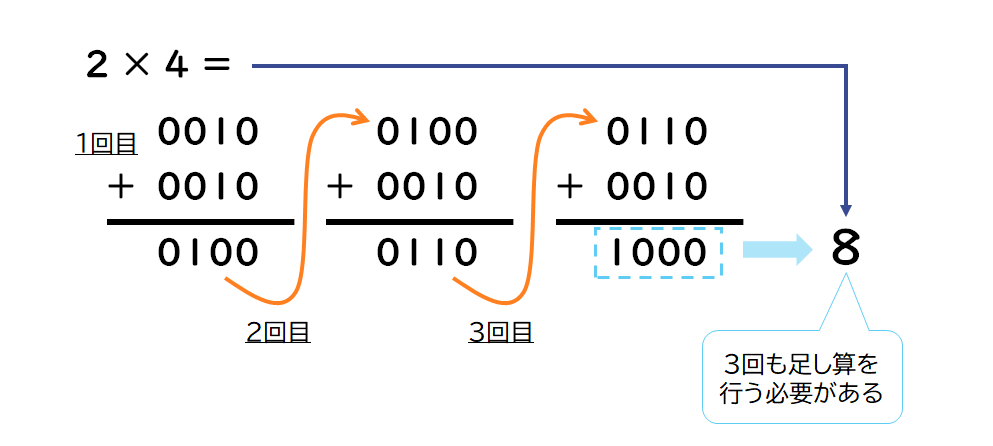
例えば「2 × 4」の場合、2の2進数表現が「0010」なので、これを4つ足せば(3回足す)「1000」になり、答えは「8」と導けます。
イメージは以下の通りです。
そして「割り算」はどうするのでしょうか?
例えば「4 ÷ 2」の場合、「0100」(10進数の4)を「0010」(10進数の2)で何回引けるかを計算すれば良いので、2回引く(2の補数を2回足す)と「0000」になり、答えは「商が2、余りが0」となります。
掛け算や割り算を行うのに何回も数字を足すのは非効率ですよね。更に桁数が大きくなれば、どんどん処理が大変になります。そこでシフト演算が出てくるのです!
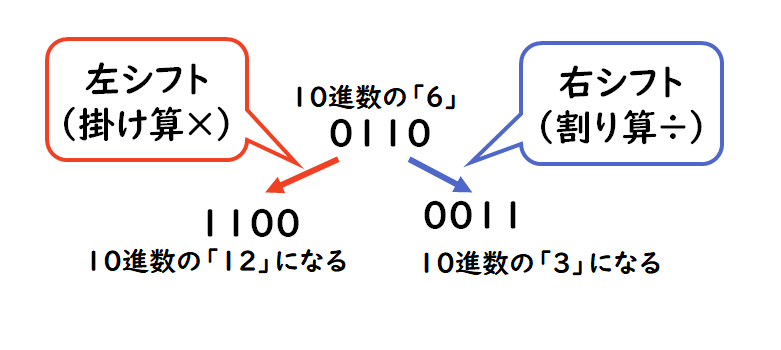
先ほどの「2 × 4」は2に4を掛けた結果、「0010」が「1000」になります。同じように「3 × 4」は「0011」が「1100」になります。よく見ると、ビットが左に2個分ずれた結果になっていることが分かります。ビットをずらす、「シフトする」ことで、簡単に掛け算の結果を出すことができます。
2進数では、「左に1つビットをずらせば2倍」に、「右に1つビットをずらせば2で割る」ことになります。
先ずはビットをずらすことで、掛け算、割り算ができることを覚えましょう!
そして、シフト演算には、符号を考慮しない「論理シフト」、符号を考慮する「算術シフト」があります。それぞれ、左シフトと右シフトがあります。
次からはそれぞれのシフト演算の違いを説明します。
論理シフトとは?
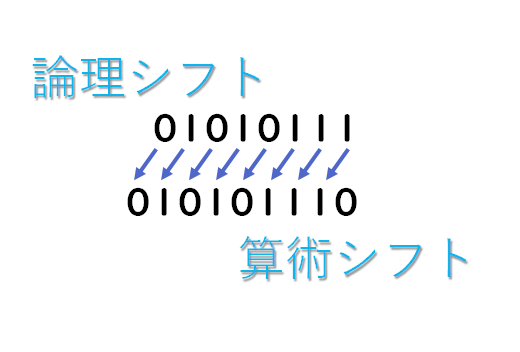
論理シフトとは、「符号を考慮しない」シフト演算のことです。2進数のビット列を左や右にずらすことで、掛け算や割り算ができます。ビットをずらすとビットの列からあふれ出てしまった分のビットは捨てられます。空いたビットは「0」で埋めます。
では、左と右にずらした時で値の計算方法が変わりますので、次にその違いを説明します!
論理左シフト
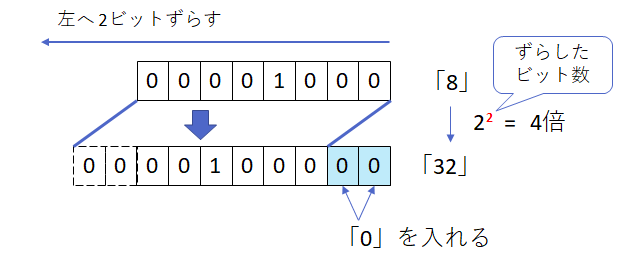
2進数のビット列をnビット左に移動すると、元の数の「2n」倍になります。例えば1ビット左だと2倍、2ビット左だと4倍、3ビット左だと8倍といった感じになります。
イメージは次のようになります。
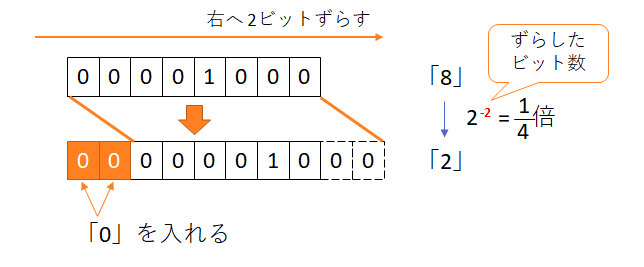
論理右シフト
2進数のビット列をnビット右に移動すると、元の数の「2-n」倍になります。例えば1ビット右だと1/2倍、2ビット右だと1/4倍、3ビット右だと1/8倍といった感じになります。
イメージは次のようになります。
算術シフトとは?
論理シフトに対し、算術シフトは「符号を考慮」します。符号は一番左にあるビットを使います。一番左のビットが1のときは、「負の数」になります。
算術シフトを行う時は符号を表しているビットは動かさずに、他のビット列の範囲を左か右にずらします。左か右によって、空いたビットの埋め方が異なりますので、次にそれぞれの違いを説明します。
算術左シフト
符号ビットは固定したまま動かさず、他のビットを左にずらします。左のあふれたビットは論理シフト同様に捨てられ、右の空いたビットには論理シフト同様に「0」が入ります。
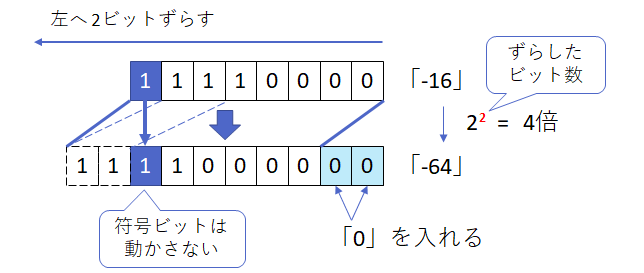
算術右シフト
上述の算術左シフトと同様に符号ビットは固定したまま動かしません。一番左より右のビットをずらします。右にあふれたビットは捨てられ、右のずらして空いたビットには符号ビットと同じ値が入ります。
論理シフトと算術シフトの使い分け
論理シフトと算術シフトの説明をしましたが、どのように使い分けるのでしょうか?
実は色々調べてみたのですが、明確な使い分けは説明されていませんでした。
算術シフトは符号で1ビット使ってしまいますので、正の演算だけしかしないのであれば論理シフトの方が扱える桁数が多くなるかと思います。反対に、負の演算もするのであれば、算術シフトを使わないといけません。
一般的には演算をする時は、算術シフトを使うようですね。
シフト演算を使った計算方法
シフト演算によって、数を2の累乗(N回)分でN倍(2倍、4倍、8倍、16倍...)することができることが分かりました。但し、実際の掛け算は3倍も5倍も6倍といった具合に色々な数を掛ける必要があります。
例えば変数Nを7倍する「N × 7」の計算を行う場合、7を2進数に分解します。
7 = 4 + 2 + 1 = 22 + 21 + 20
Nに7を掛けるので、次のようになります。
$$\begin{align*} N \times 7 &= (N \times 2^{2}) + (N \times 2^{1}) + (N \times 2^{0}) \\
&= (Nを2ビット左へ)+(Nを1ビット左へ)+(Nを0ビット左へ)\end{align*}$$
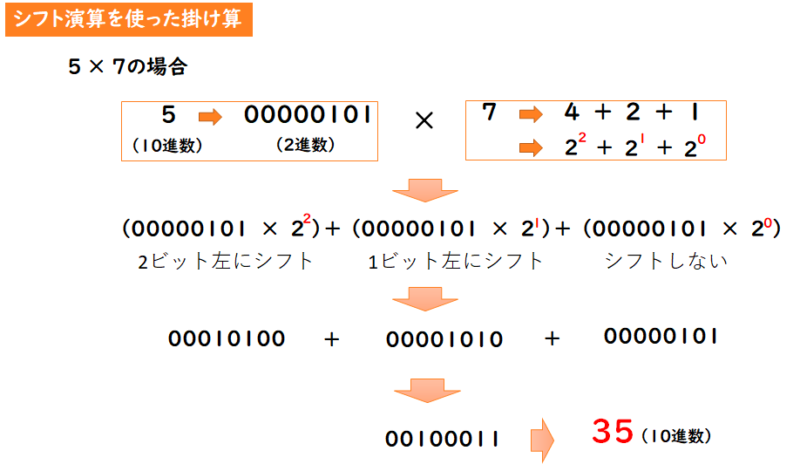
「5 × 7」の場合。
$$\begin{align*} 5 \times 7 &= (00000101 \times 2^{2}) + (00000101 \times 2^{1}) + (00000101 \times 2^{0}) \\
&= 00010100 + 00001010 + 00000101 \\
&= 00100011 \\
&= 35(10進数) \end{align*}$$
このようにして掛け算は、「2n同士の足し算に置き換えて計算」を行います。
次に割り算です。
こちらは、掛け算の逆で「2nの引き算を使って計算」を行います。割られる数字に対して、割る数字を使って何回引けるか考えて計算します。
掛け算に比べてちょっと考え方が難しいです。
例えば「20 ÷ 4」の場合は、20を2進数にすると「00010100」(20)となり、ここから4の2進数の「00000100」(4)を引きますが、「00000100」を左に2ビット、つまり22ずらして、「00010000」として引きます。
そうすると、20は「00000100」となります。さらに4の「00000100」をシフトしない、つまり20として、引きます。そうすると20は「0」になって、計算は終了となり、商が「22 + 20 = 5」となります。ちょっと文字だけだと、分かり難いですね...
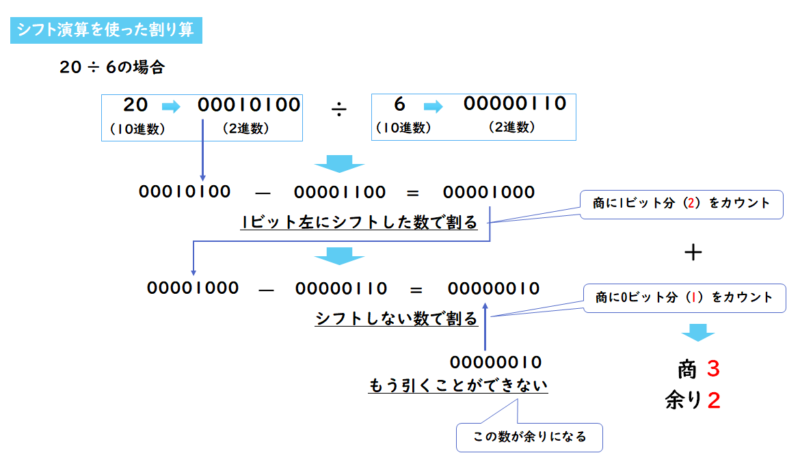
余りが発生する割り算として「20 ÷ 6」の場合は、同様に「00010100」(20)から6の2進数「00000110」を左に1ビットシフトして引きます。「00010100」が「00001000」になり、更に「00000110」で引くと、「00000010」となり、これ以上は「00000110」で引けないので、計算が終了となります。この計算の商は「21 + 20 = 3」で余りは「00000010 」なので「2」となります。
やはり、文字だと分かり辛いので、図で描いてみました!
まとめ
今回はコンピュータにおける掛け算や割り算を簡単にするためのシフト演算に関して解説しました。
ビットをずらすにも勿論回路が必要なので、掛け算をするのに、何回も数を足し合わせるよりは遥かに処理が速くなり、これは大きなメリットになりますね。
普段コンピュータ使っていてシフト演算を意識することは無いと思いますが、プログラミングでは使うことがありますので、しっかり理解しておきましょう。
以上です!