みなさんは試験の合格発表で一覧から自分の番号を探す時、どうやって探しますか?
一覧の上から一つずつ見るより、ざっくりこの辺りだな、ってところから探し始めると思います。そして番号が近付くとドキドキすると思います。つまり、効率的に番号を探索していますよね。
コンピュータがデータを探す時も同じように効率的に探索してます。
そこで出てくるのが、「探索アルゴリズム」というもので、何か難しそうですが、実はそんなに難しくないです!
ただ、効率的な探索アルゴリズムを作るためには効率的にデータを格納しておく「データ構造」がポイントとなります。
そのデータ構造の一つとして「木構造」がありますので、今回は木構造の仕組みや探索アルゴリズムの使い方に関して解説します!
木構造とは?
まず、木構造は、データ同士に階層的な親子関係をもたせたデータ構造のことを意味します。「ツリー(木)構造」とも言いますね。
この木構造ですが、図に書き表すのが一番分かり易いです。
下の図を見て頂くと、「樹木を逆さ」にしたような形になっていることが分かりますね。
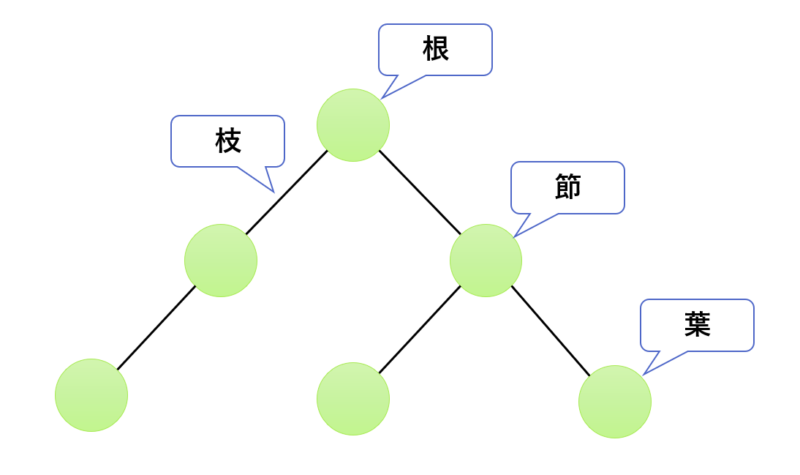
木構造の各部分
- 節(ノード):木構造における各データ部分
- 根(ルート):節の中で木の根っこにあたる一番上の部分
- 葉(リーフ):節の中で木の一番下の部分
- 枝(ブランチ):節と節をつなぐ経路
木構造の親子関係
木構造においては、データは親子関係になっています。
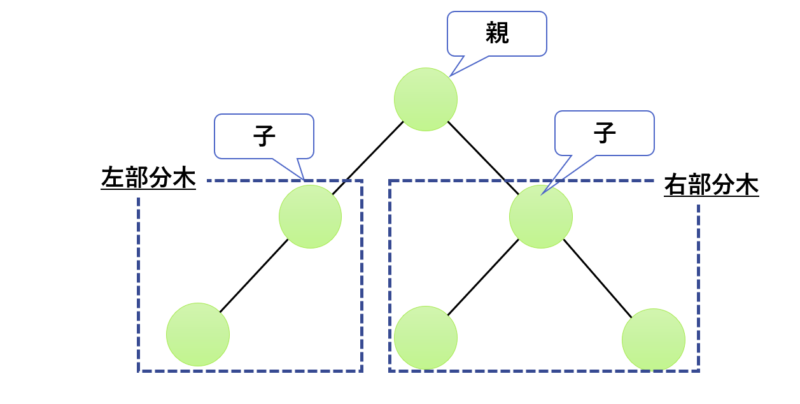
枝で結ばれた二つの節において、上の節を「親」、下の節を「子」と呼びます。子の下に節があれば、その節は親になります。家系図みたいなものですね。
また、親の節から見た場合に、左の子についている「節(葉)、枝」をまとめて「左部分木」と呼び、右の子についている「節(葉)、枝」をまとめて「右部分木」と呼びます。
2分木のデータ構造
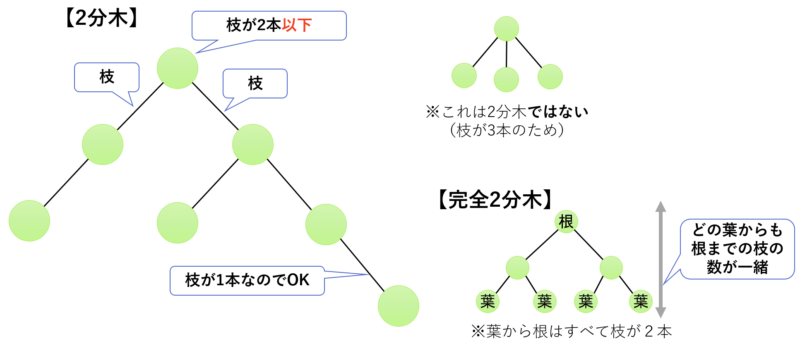
木構造において、根やそれぞれに節から出る枝が、「すべて2本以下」になる木を「2分木」と呼びます。枝が3本以上になると、それは2分木では無いことになります。
更に、2分木の中でも、根から葉までの枝の数がすべて一緒になる2分木を、「完全2分木」と呼びます。
2分木のデータ構造
冒頭に2分木は「データ構造」の一つと記載しましたので、データ構造として2分木を見てみます。
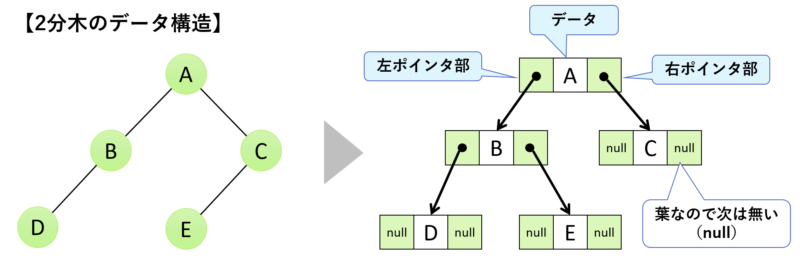
2分木の節はそれぞれ以下の3要素に分けられます。
2分木のデータ構造
- 左ポインタ部 : 子の節の場所情報が格納される
- データ部 : データが格納される
- 右ポインタ部 : 子の節の場所情報が格納される
イメージは以下のようになりますね。
このデータ構造を使うことで、データを効率的に検索することができます。
続いてその探索手法を解説します。
2分探索木を使ってデータを探索する
2分探索木(にぶんたんさくぎ)とは2分木の中で、以下のルールに則っている状態の木のこととなります。
全ての節で親のデータが左部分木のデータより大きく、右部分木のデータよりも小さい
(左部分木のデータ < 右部分木のデータ)
このルールに則った2分探索木は、親より左には小さいデータしかなく、右には大きいデータしかないので、必要なデータを探索する時に判断の数を少なくする、つまり処理の数を減らすことができるという特徴があります。
例として下の図を見てみましょう。
要素(データ)が「1,2,4,5,7,10,12,13」の8つあります。二分探索木としては、「根」が「5」になり、根から見たら、左部分木には「1,2,4」、右部分木には「7,10,12,13」が存在するようになります。
次に左部分木においては親が「2」になり、そこの左部分木には「1」、右部分木には「4」を置くことで、二分探索木のルールが成立するようになります。
この状態でデータ探索を行ってみましょう。
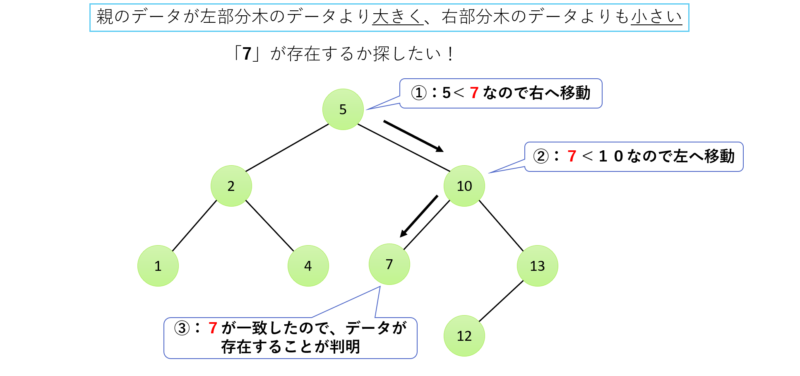
このデータの中に「7」が存在するか調べたい時に、先ずは探しているデータと根の値を比較します。
根である「5」と「7」を比較した時に「(根)5<7(探索データ)」が成立するので、探索しているデータは右部分木にある可能性があるので、次は右部分木の中を探索します。
右部分木の節である「10」と「7」を比較した場合「探索データ(7)<10(節)」となるので、左に進みます。
そうすると、「7」が見つかりますので、このデータの中には「7」が存在することが判明します。
線形探索法と呼ばれる探索アルゴリズムは、先頭から順番に目的のデータと比較し、一致するデータを探していきます。「1,2,4,5,7,10,12,13」の要素から7を探した場合、5回目にデータを見つけることができます。
これが2分探索木を使うと3回の処理で探すことができるので、探索効率が良いことが分かりますね。
まとめ
今回は木構造の仕組みと2分木のアルゴリズムを使ってのデータ探索に関して解説してきました。
木構造まとめ
- 木構造とはデータ構造の一つ
- 節(根、葉)、枝の要素を持つ
- 枝が二つ以下の木を2分木と呼ぶ
- 2分探索木を使うことでデータを効率的に探索できる
木構造は様々な用途があり、ディレクトリツリー、ドメイン名などのデータを操作する時や、データをソートする際にも使われていますので、しっかりと理解しておくと良いですね。
以下の記事でアルゴリズムそのものに関して解説してますので、併せて読んでみてください。
以上です!
-

-
あわせて読むアルゴリズムとフローチャートを理解しよう!
続きを見る