固定小数点数と浮動小数点数の違いを調べよう！

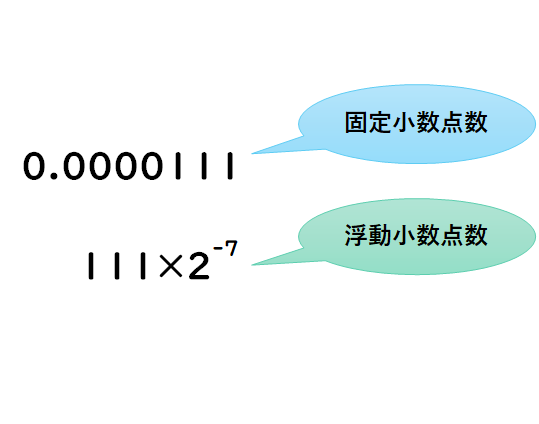
2進数の計算で「小数点」が出てくるとちょっとハードルが上がる感じがしますが、今回はコンピュータにおける小数点の表現方法の「固定小数点数」と「浮動小数点数」について解説します！

【固定小数点数表示】0.00000015

【浮動小数点数表示】0.15×10^-6

固定小数点数とは？

2進数で小数点を扱う際に何ビット目（何桁目）が小数点になるかあらかじめ決めておく方法です。

普段私たちが数字を計算する時は当たり前のように小数点の位置は決めて計算してますよね。それと同じことをコンピュータでも行うだけです。

例えば2進数の「101.01」を8ビットの固定小数点数で表現するときに、4桁目の後を小数点の場所と決めると、次のようになります。

0101.0100（4桁目に小数点が固定されている）

加算や減算をするときもこの形式に合わせた数を利用して計算します。また、一番左のビット（最上位ビット）を符号ビットとすることで、負数も表現できます。

固定小数点数の場合、小数点の位置がきまっているためデータの解釈は簡単になるのですが、その代わり、表現できる数値の範囲が限られてしまいます。

例えば先ほどの4桁目の後ろが小数点と決めると最大で「1111.1111」までの数字しか表現できなくなり、符号なしで10進数ですと「15.9375」までしか表現できません。

このためもう一つの表現方法である浮動小数点数があるのですが、固定小数点数はどこで使われるのでしょうか？その答えは次にあります。

固定小数点数の利用方法、それはズバリ整数を表す時に利用します！

整数をあらわすには、最下位ビットの右側を小数点とする、と決め打ちにしています。これにより、小数部に割くビットの数を無くして、整数だけを扱うことになるわけですね。

つまり、「00000000.」と表現する訳です。

コンピュータの整数は小数点が一番右にある数になりますね。

続いては、浮動小数点数です。

こちらは固定小数点数で制限されていた表現できる数値の範囲を広げるための方法です。

範囲を広げるために、指数部と仮数部を用いた指数表記を使って数を表します。ちょっと分かり難いと思いますので、例を上げると次のようなことです。

10進数（10が基数）の「0.00025」は、「2.5（仮数部）× 10^{-4（指数部）}」で表現できます。

この表現の方法ですが、仮数部と指数部を変えることで、様々な表現ができます（上の例だと0.25× 10^-3でも良い）。この時に、より有効桁を多くとれるように（範囲を広げるために）小数点の位置を調整して、仮数部の最上位桁を0以外の数値にすることを正規化といいます。

2進数の場合は2が基数となりますので、記号で表現すると以下のようになります。

±(符号) m(仮数) × 2(基数)^e^(指数)

例えば、「-0.1011×2^-5」という数字があった場合、符号は負なので「1」、仮数部は「1011」、指数部は「-5」と区別して、それぞれ保管して表現すれば良いのです。

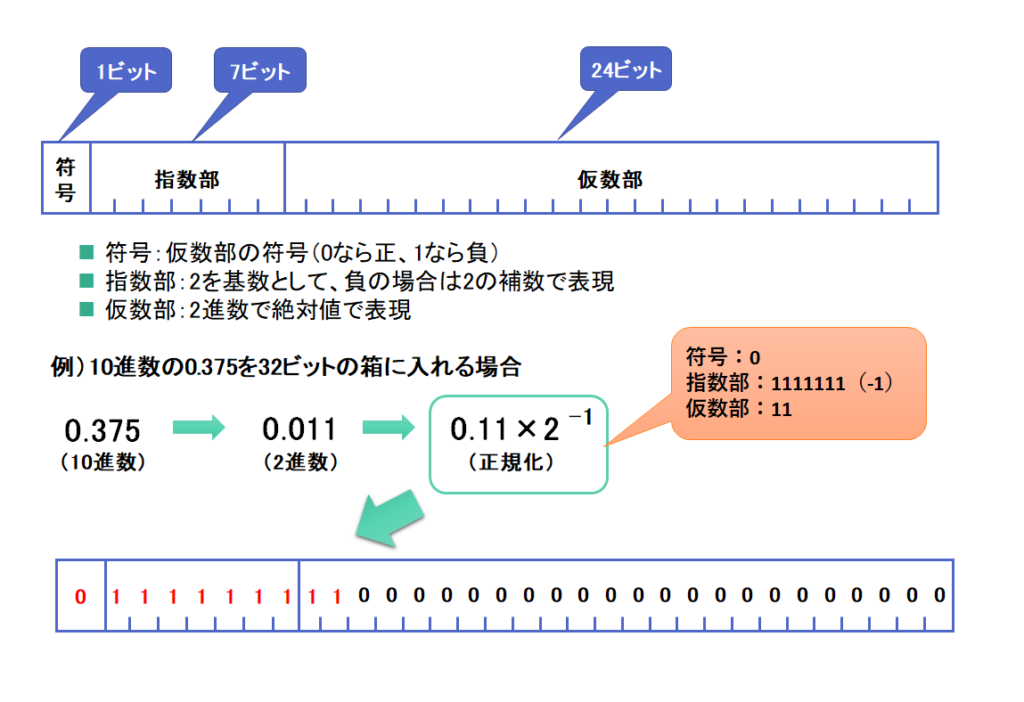
実際32ビット形式で浮動小数点数を表現する時の例を図にしてみましたのでこちらをご覧ください。

浮動小数点数におけるメリットは「非常に大きな値から非常に小さな値まで使うことができる」ということですが、デメリットは何なのでしょうか？

デメリットとしては「計算が近似値計算なので誤差が発生する」ということです。簡単に言うと、決められた桁で値を表現するため、はみ出た分は正確に表せないことになってしまいます。これを誤差と呼びます。

固定小数点数は0に近いほど有効桁数が減ってしまいますが、演算の過程で有効桁数を失うことはありません。一方、浮動小数点数は有効桁数は規格化によって一定になりますが、演算の過程で数値を失ってしまうこともあります。

IEEE（米国電子電気技術者協会）により規格化された、IEEE754という浮動小数点数形式があります。この形式は仮数部を「1.仮数部」の形で正規化することで、先頭の1を暗黙的に省略することができ、その分、前の例の「0.仮数部」の形よりも1ビット多く保持することができ、表現の幅が広がります。

また、バイアスという処理も行います。バイアスとは「偏り、かさ上げ」などの意味がありますが、この場合は「かさ上げ」することです。

指数部にバイアスをかけることで、負の数を含む表現が全て正の数だけで表せるようになりますので、数の大小表現が分かり易くなります。

こちらは以下サイトを参考にしてみてください。

今回はコンピュータの中の小数点表現である、固定小数点数と浮動小数点数を解説しました。

掘り下げると奥が深いですが、コンピュータの計算をシンプルにするためには必要な考え方ですね！

また、プログラム言語においては、型の宣言によって、どちらの小数点表現が使われるか決まるようです。

C言語やC++、JAVA言語などで用いられるfloat型、double型は、浮動小数点数表現を使うデータ型です。

一方、COBOLなどの事務処理系の言語では、固定小数点数表現が使われることが多いみたいですね。

以上です！

参考URL）