コンピュータの勉強を始めるぞ!となって、基礎理論を学び始めると2進数という言葉と共によく最初に出てくる基数という言葉ですが、普段あまり使わないので、急に出てくると「うっ!」ってなることがあります。
今回はそんな基数をシンプルに解説します!
頭の中にコンピュータで使う「基数」という言葉をしっかり頭の中にインプットしましょう。
コンピュータの内部で扱うデータ形式
コンピュータを使う時、私たちはキーボードから文字や数字を入力して、様々な処理をコンピュータにしてもらってますが、入力する文字や数字は紙に書いたり、計算したりすときに使うものと同じです。
しかし、コンピュータ自身は、電気回路でONとOFFの二パターンでしか扱うことができません。そのため、我々が入力した複雑な文字や数字はコンピュータの中でONとOFF、すなわち「1」と「0」を使って変換された上で、処理されているのです。
この「0」と「1」の二つのパターンを使うことを「2進数」と呼びます。コンピュータの内部で最終的に使われる数は2進数です。先ずはこの考え方を覚えておきましょう。
基数とは?
コンピュータは数字を二つの数で全てを表すので「2進数」ですが、私たちは「0~9」までの10個の数字で数を表すので、これを「10進数」と呼びます。
2進数も10進数も桁数が多くなればなるほど、表現できる数は多くなります。
では、2進数と10進数の関係はどうなっているのでしょうか?下の図に対応を表現してみました。
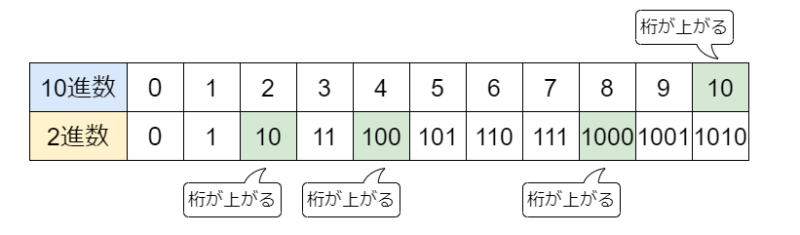
2進数の1桁で表現できる数は0と1の二つですが、2桁になると「00,01,10,11」の四つの数が表現できるようになり、3桁になると「000,001,010,011,100,101,110,111」の八つの数が表現できるようになります。つまり、桁数が増えると表現できる数が指数関数的に増えていきます。
そして、10進数も同じように桁が増えていくと表現できる数が増えていきます。
はい。ここで、やっと基数を説明になります!
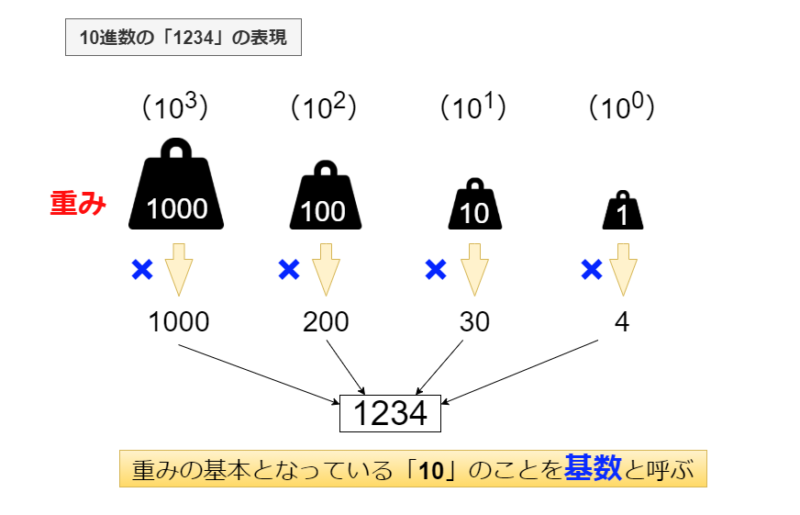
上図のように、重みは全て10の「累乗」で表されます。この重み付けの基本となる値のことを「基数」と呼びます。
基数とは?
- 重み付けの基本となる数
- 桁上がりの基準になる数
2進数から10進数への変換
2進数の場合は基数は「2」となります。
重みは小数点を起点として整数部は「20、21、22」といった形に増えていき、小数点以下は「2-1、2-2、2-3」と減っていきます。
2進数の各桁の数字にこの重みの値を掛けていけば、2進数を10進数へ変換できます。
下の例は(101.01)2という2進数を10進数に変換すると(5.25)10になるという例です。
(※数値をカッコで囲んで後ろに添え字を付けることで2進数や10進数表現を明示します)
10進数から2進数の基数変換
では、逆に10進数から2進数への変換はどうやるのでしょうか?
これは10進数の整数部と小数部で変換の方法が異なり、ちょっと面倒です。
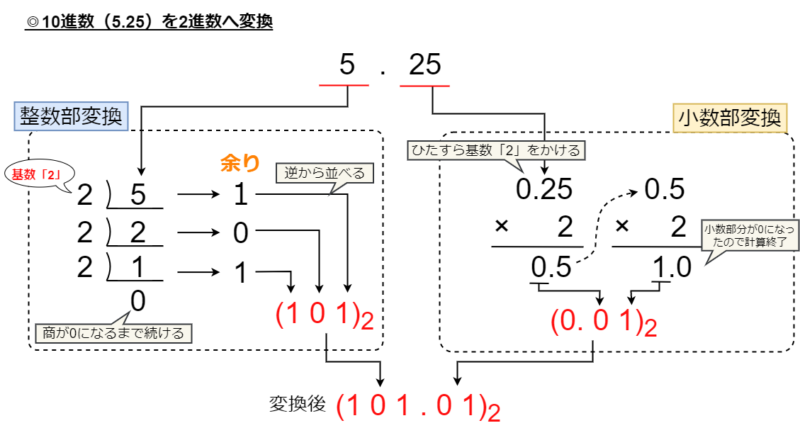
先程の例に出てきた10進数の「(5.25)10」を2進数に変換してみましょう。
先ずは整数部「5」の変換ですが、「5」を2進数の基数である「2」でひたすら割って、商が0になるまで続けていきます。そして、それぞれの計算で出た「余りの数(0か1)」を逆から順に並べることで2進数にすることができます。この場合は「(101)2」となります。
次に小数部の「0.25」の変換ですが、ここでも2進数の基数である「2」でひたすらかけ算をしていき、その結果の「整数部分を取り出し」ます。これを小数部分が0になるまで繰り返してて、取り出した整数部分を小数第1位から順に並べていくことで、2進数へ変換ができます。この場合は「(0.01)2」となります。
最終的には整数部と小数部を結合して、「(101.01)2」が10進数「(5.25)10」を2進数に変換した結果になります。
下に変換の流れを図にしてみました。ちょっと分かり辛いですが、計算方法を覚えてしまうのが手っ取り早いですね。
まとめ
今回はコンピュータの数字の基礎となる基数を解説してみました。
基数は重み付けの基本になる数字であることが分かったかと思いますが、2進数から10進数への変換やその逆変換を行うときに使うことができますね。
コンピュータの世界では他に8進数や16進数もありますが、同じく基数は「8」や「16」になります。これらの変換方法はまた別のやり方がありますので、そちらも理解しておくと良いかと思います。
我々が日常使っている10進数の数字やひらがなや英文字の入力をコンピュータは最終的に2進数に変換し凄い速さで処理しているのですね。実際に進数の変換を手で計算してみるとその凄さが改めて分かりますね。
コンピュータに感謝ですね!
以上です!