情報処理と言えば論理演算!ってくらい、よく出てくる言葉で、ネット上にも色々解説がありますが、結構奥が深い話なので、今回は初めの一歩を理解するために、シンプルに解説します!
命題と論理演算の目的とは?
コンピュータの計算や処理は「算術演算」と「論理演算」によって実行されています。
算術演算は、「ビットを使っての足し算や引き算を行う 」処理のことで、算数的なイメージですね。
一方、論理演算は、「ある事柄が真か偽か」を判断する処理です。コンピュータが理解できる数値に置き換えると真のときは1、偽のときは0という形になります。
この真偽(真:True、偽:False)を評価することの条件のことを「命題」と呼びます。例えば、「マウスをクリックしている」という命題に対して、「True(1)」、「False(0)」という評価があるようなイメージです。
コンピュータは色々な命題を組み合わせる、すなわち論理演算を行う回路(論理回路)を作り、それらを組み合わせていくことで、複雑な処理ができる(最終的な命題の結果を出す)ようになってます。
それでは、この論理演算と関係する論理回路や真理値表、集合の中身に進みましょう!
論理回路と表記法
冒頭でも述べましたがコンピュータの中には論理演算を行うための論理回路が組み込まれています。この回路は電気信号を使って演算する装置で、遥か昔はコイルやスイッチを使ったリレー回路や真空管を使ってましたが、現在は半導体を使ったトランジスタやダイオードで作られています。
そして、この論理回路は図にした時に一目で分かり易いように記号を使って表現されています。この記号のことを「MIL記号(ミル)」と呼びます。
また、論理演算の条件と答えを一覧にした「真理値表」や、ある条件で集まったグループ「集合」を色を塗って図で表す「ベン図」も使って論理回路を表現していきます。
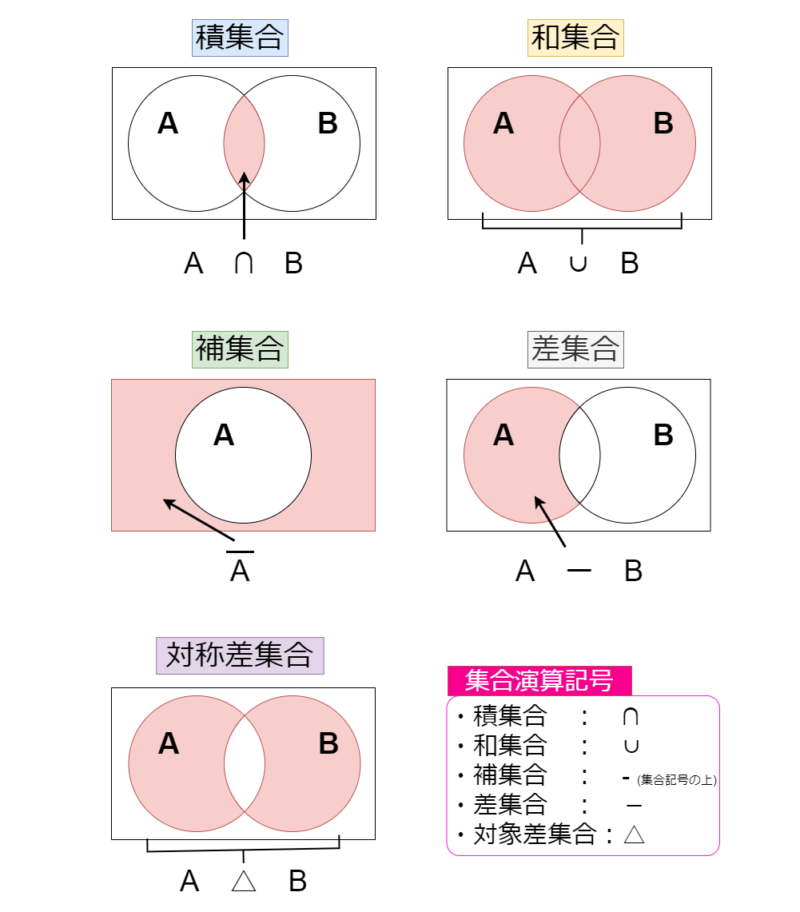
ベン図を理解しよう!
先ずはベン図を理解しておくとこの後の話に入り易いです。
集合とは「ある条件に合致して、他と区別できる集まりのこと」であり、この集合と集合との関係を表すためにベン図を利用します。
ベン図は主に円を用いて各条件に合致した集合を表し、その円と円の関係を塗りつぶしたりして関係性を表現しています。
基本回路とは?
論理演算のもっとも基本的な演算ルールが論理和(OR)、論理積(AND)、否定(NOT)の3つの論理演算となります。
この3つを理解すれば、複雑な論理演算もこれらの組み合わせで実現できますので、しっかり理解しましょう。
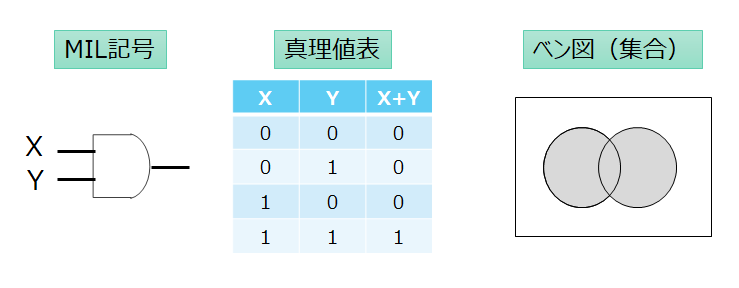
論理和(OR)
先ず論理和ですが、これは入力される二つの値(X,Y)のどちらかが「1」ならば、結果(答え)が「1」になる論理演算です。
どちらも「0」のときだけ、結果が「0」になります。
演算式は「X+Y」となります。(「+」の記号を使う)
真理値表とベン図は以下のようになります。
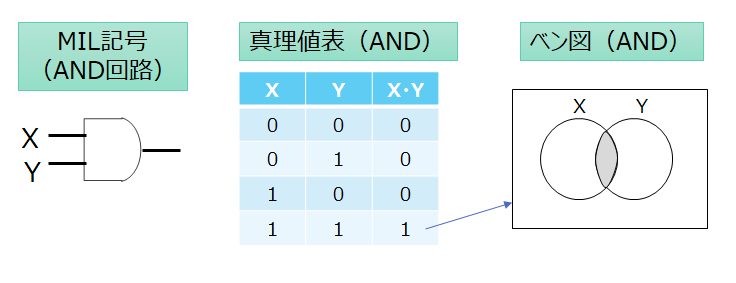
論理積(AND)
続いて論理積ですが、これは入力される二つの値(X,Y)のどちらも「1」だった場合に、結果が「1」になる論理演算です。
どちらかが「0」だったり、どちらも「0」の場合、結果が「0」になります。
演算式は「X・Y」となります。(「・」の記号を使う)
真理値表とベン図は以下のようになります。
否定(NOT)
最後に否定ですが、これは入力Xが「0」の場合、結果が反対の「1」になります。反対に入力Xが「1」であれば、結果が「0」になる論理演算です。
演算式は「X 」となります。(「¬」の記号を使う)
真理値表とベン図は以下のようになります。
基本回路の組み合わせ
3つの基本回路(論理和、論理積、否定)を組み合わせることで、以下の3つの回路を作成することができます。
排他的論理和(XOR)
「排他的論理和」ってちょっと難しい言葉ですが、入力のXとYが異なる時に結果が「1」になり、同じとき(1と1か0と0)の時に結果が「0」になる論理演算です。
真理値表とベン図は以下のようになります。
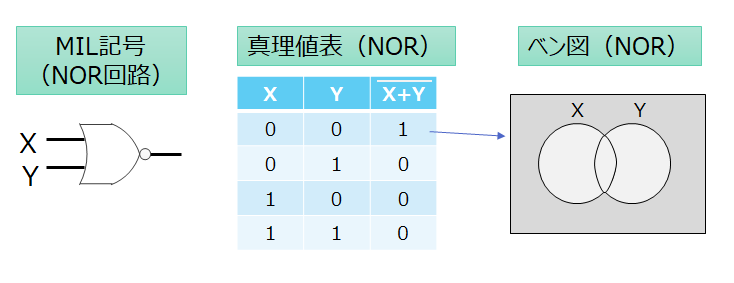
否定論理和(NOR)
否定論理和は、入力のXとYがどちらも「0」の時に結果が「1」になり、その他の組み合わせの時の結果が「0」になる論理演算です。論理和と否定の組み合わせとなります。
真理値表とベン図は以下のようになります。
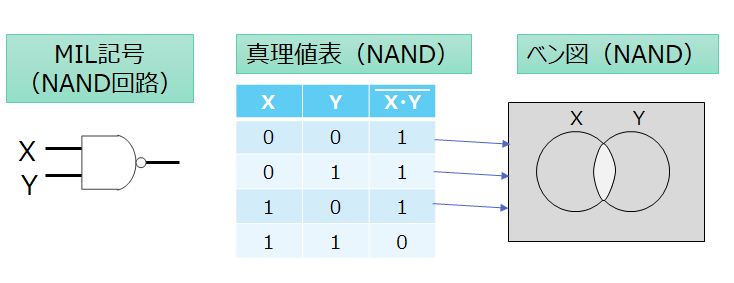
否定論理積(NAND)
否定論理和は、入力のXとYがどちらも「1」の時に結果が「0」になり、その他の組み合わせの時の結果が「1」になる論理演算です。論理積と否定の組み合わせとなります。
真理値表とベン図は以下のようになります。
まとめ
今回は命題と論理演算の関係、それを使った論理回路や真理値表、集合(ベン図)を解説してきました。
論理演算には色んなパターンがありますが、基本的には論理和(OR)、論理積(AND)、否定(NOT)の組み合わせを使って表現できるのですね。
論理演算の考え方はコンピュータの基礎であり、プログラムやデータベースの設計にも繋がっていくので、しっかりと覚えておく必要がありますね。
以上です!