コンピュータは2進数で計算していますが、扱える2進数は無限では無い(有限)ため、2進数を何桁まで使うかはコンピュータの性能などによりあらかじめ決められています。つまり、桁数が多い数字などは現実の値をコンピュータ上では正確に表せない場合があります。
では、そんな時はどうするかと言うと、コンピュータの中で近似値に置き換えられてしまいます。近似値なので実際の値と差がでます。この差のことを「誤差」と呼びます。
今回はこの誤差が発生する原因とその種類を解説します!
コンピュータの様々な誤差
早速、色々な誤差を解説していきます!
桁あふれ誤差とは?
コンピュータが計算した結果の桁数が扱えるビット数を超えてしまうことによって発生する誤差のことです。
ビット数の最大値を上回る桁あふれのことを「オーバーフロー」、最小値を下回る桁あふれを「アンダーフロー」と呼びます。
例えば、8ビットの固定小数点の場合に値の範囲は「-128 ~ 127」になります。計算結果として、この範囲をはみ出してしまった場合がオーバーフローとなり、コンピュータで値を表現できなくなってしまいます。
一方、浮動小数点を扱う場合、指数部(桁数)には限界があります。「0.000000000000000000000000000000000……00001」のように限りなく0に近い値の場合、指数部の限界を超えてしまい、この値もコンピュータで表現できなくなってしまいます。これがアンダーフローです。
丸め誤差とは?
限られた桁数の範囲で数値を表現する時に、切り上げや切り捨て、四捨五入などを行って、桁を削ったことで発生する誤差のことです。
例えば「1.2345678912345...」と無限に数字が続く数字があった場合に有効桁数が7桁だとすると、頭の「1.234567」で切り捨てを行います。
そうすると「0.0000008912345...」分が丸め誤差となります。
打切り誤差とは?
この誤差は計算を途中で打ち切ってしまうことで発生する誤差のことです。
よくある例ですが、円周率は「3.141592...」と続いていきますが、永遠に計算が続いてしまうので、あらかじめ決めておいた桁数で計算処理を途中で打ち切って、計算結果を「3.14」として扱うことがあります。
この際に発生する 「3.141592...」 と「3.14」の差が、打切り誤差となります。
桁落ちとは?
絶対値のほぼ等しい2つの数の引き算を行ったときに、有効桁数が減少するために発生する誤差のことです。
この桁落ちなんですが、ちょっと捉えにくいです。
例えば、有効桁数が4桁の場合に①「1.2345」と②「1.2334」という数値の差を計算するプログラムがあるとします。
この場合、先ず元の数字を4桁にするために①「1.2345≒1.234」、②「1.2334≒1.233」となります。
ここで①-②を計算すると「1.234 - 1.233 = 0.001」となります。その結果、有効桁数が4桁から1桁に減少してしまいます。
ここで、コンピュータは「0.1000 ×10-3」のように、仮数部が4桁になるように0で埋めてしまいます。 そんなに悪いことのようには思いませんが、元々の5桁の数値で計算すると、「1.2345 - 1.2334 = 0.0011」なので、有効数字が4桁のままなら、「0.1100 ×10-3 」となり、0で埋めた結果とは違うことになります。
この埋めた「0」が元々0であったかどうかは保証されない状態になってしまいます。
この桁落ちですが、計算結果が限りなく小さい値なので、それこと誤差の範囲としては問題無いと思われますが、桁落ちされた数値を使って更に計算する時が問題となります。
桁落ちの結果の数値に10万倍など大きな数字を掛けるとこの誤差の値が膨れ上がってしまうことになります。
桁落ちへの対応としてはデータ型としてdouble型を用いたりすれば精度が上がりますね。
上記説明はあくまで概念的な話ですので、実際のコンピュータ上の処理とは別であることをご了承くださいね。
ということで、桁落ちは理解するのが難しいですね。。。
情報落ちとは?
情報落ちは桁落ちと反対のイメージとなります。
絶対値の大きな値と絶対値の小さな値の足し算や引き算を行った際に、小さな値の桁情報が無視されてしまい、計算結果に反映されないことで発生する誤差のことです。
コンピュータで扱う浮動小数点数では、仮数部に保持できる数が予め決められています。そのため、大きな値と小さな値の足し算や引き算をを行うと、有効な数字を持った桁が大きくなり過ぎてしまい、正規化する際に下部の桁が切り捨てられてしまうことになります。
例として、数値を扱うときに有効桁数が4桁の場合、①「1.234×103」と②「1.234×10-2」という足し算を行ってみます。
実際の値を計算すると「1234+0.01234 = 1234.01234」となりますが、コンピュータのプログラム上は指数部を揃えて計算するので、①+②は「1.234×103 +0.00001234 ×103=1.234 × 103 」となり、仮数部の下部の桁が切り捨てられてしまい、実際の値とは0.01234の誤差が発生していしまうことになります。
誤差の種類を整理する!
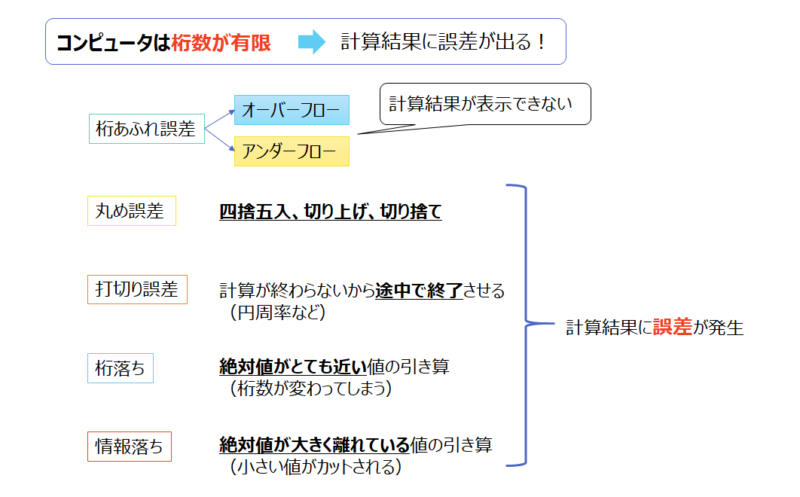
色々な誤差の種類が出てきましたが、種類が多いので、イメージにしてみました。
オーバーフローやアンダーフローなどのように値がコンピュータで表現できなくなるパターンと計算結果に細かい違いが出るパターンに分けられますね!
まとめ
今回はコンピュータにおける誤差に関して解説してきました。
どれも誤差には変わり無いのですが、発生する原因によって種類が違うのですね。
コンピュータを使う限り計算できる桁数は有限なので、誤差が発生するのは仕方ないことですが、誤差の影響を極力少なくするためにデータの型を変えたり、エラー処理を工夫するなどの対策が重要なのですね。
そして誤差が発生するポイントとしては、「コンピュータには有限の桁数がある」ということですかね。
以上です!
参考URL)桁落ちってなんぞ?( 技術系のど根性 )