システムの信頼性を計るための数値として「稼働率」があります。システム単体の稼働率を求めるには、以下の方法で求めることができます。
$$稼働率 = \frac{MTBF}{MTBF+MTTR} = \frac{全運転期間の中でシステムが故障していない時間}{システムの全運転期間}$$
詳しくは以下記事をご参照ください。
では、色々なシステム(例えば、メールサーバ、DNSサーバ、プロキシサーバなど)を組み合わせて、一つの大きなシステム(サービス)と定義した時の稼働率はどうなるのでしょうか?色々なシステムを組み合わせるということは、稼働率がそれぞれ違うシステムや複数のサーバが存在することになります。
また、可用性を持たせるためにサーバを複数台用意することもあります。
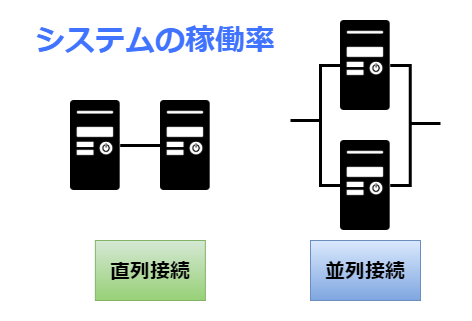
この大きなシステム(サービス)の構成は様々な形になりますが、突き詰めると結果的にシステムやサーバを「直列」や「並列」に接続していることになります。
今回はこのシステムを直列や並列に繋いだ際の稼働率の計算方法について解説します!
直列接続の稼働率の算出
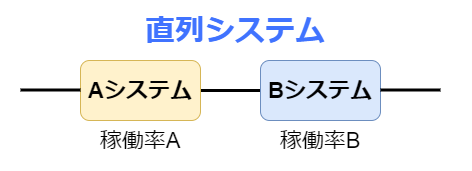
システム同士を直線状に接続したシステムのことを「直列システム」と呼びます。
システムを直列に繋いだ場合、どれか一つのシステムで障害が発生すると、システム全体が稼働しなくなってしまいます。
この直列システムにおける稼働率の計算方法は以下のようになります。
$$稼働率 = Aシステムの稼働率 \times Bシステムの稼働率$$
例えば、Aシステムの稼働率が「0.95」、Bシステムの稼働率が「0.9」の場合全体の稼働率は以下の通りとなります。
$$稼働率 = 0.95 \times 0.9 = 0.855$$
あるシステムの稼働率が非常に低いとシステム全体が止まってしまう確率が大きくなってしまいますね。
並列接続の稼働率の算出
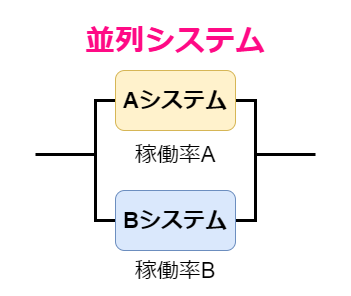
もう一方、並列にシステムを接続したものを「並列システム」と呼びます。
システムを並列に接続することで、接続したシステムやサーバの一つでも稼働していれば、システム全体は稼働し続けることができます。
そのため構成するシステムの稼働率が同じ場合は、先に説明した直列システムよりも並列システムの方が稼働率は高くなります。
並列システムにおける稼働率の計算方法は以下のようになります。
$$稼働率 = 1-(1- Aシステムの稼働率) \times (1- Bシステムの稼働率)$$
例えば、Aシステムの稼働率が「0.95」、Bシステムの稼働率が「0.9」の場合全体の稼働率は以下の通りとなります。
$$稼働率 = 1-(1-0.95) \times (1-0.9) = 1-(0.05 \times 0.1) = 0.995$$
因みに「1 - 稼働率」は「故障率」と呼ぶことができます。
並列接続したシステムの中で稼働率が非常に高い(故障しない)システムがあると、システム全体としても稼働率が高くなることになりますね。
複雑なシステムの稼働率
直列システムと並列システムの稼働率を学んだところで、これらを組み合わせた時の稼働率を求めてみましょう。
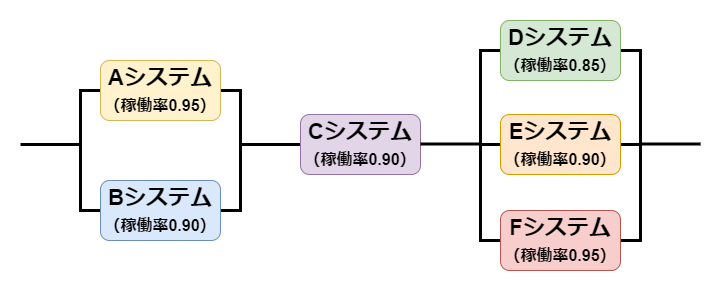
下の図にあるような複雑なシステム構成の稼働率はどうなるでしょうか?
先ずは並列接続しているシステムの稼働率をそれぞれ求めます。
$$\begin{align*} A・Bシステムの稼働率 &= 1-(1-0.95) \times (1-0.9) \\
&= 1-(0.05 \times 0.1) = 0.995 \end{align*}$$
$$\begin{align*} D・E・Fシステムの稼働率 &= 1-(1-0.85) \times (1-0.9) \times (1-0.95) \\
&= 1-(0.15 \times 0.1 \times 0.05) = 0.99925 \end{align*}$$
それぞれの稼働率を直列接続として、稼働率を求めます。
(※小数点6位を四捨五入)
$$\begin{align*} 全体の稼働率 &= A・Bの稼働率 \times Cの稼働率 \times D・E・Fの稼働率 \\
&= 0.995 \times 0.9 \times 0.99925 ≒ 0.89483 \end{align*}$$
このように、先ずは並列接続の稼働率を求めて、その後直列接続で稼働率を求めるのがポイントですね。
まとめ
今回はシステム全体の稼働率に関して解説してきました。
システムやサーバーを直列に繋いだ時と並列に繋いだ時でそれぞれの稼働率に違いが出ることが分かりましたね。並列繋ぎの方が稼働率は高くなりますが、並列繋ぎにするとコストも仕組みも複雑になりますので、何でもかんでも並列繋ぎって訳にはいきませんね。
また、他のシステムの障害の影響を受けないよう、システムを独立させてたり、サーバを多重化することも大事ですね。
小学生の頃、豆電球の直列繋ぎ、並列繋ぎを習いましたが、あれと同じで、直列に繋いだ豆電球の一つが切れたら、他も切れてしまう(電流が流れなくなる)原理ですね。
以上です!